・数値微分とその精度

　計算機上で数値的に微分を行うとはどういうことでしょう？私たちはある種の関数に対してはその微分がどういう関数で与えられるかを知っています。しかし、一般的には私たちになじみのある初等関数ばかりを相手にするわけではないですし、時には関数形すら与えられていないデータについても微分値が欲しくなることもあるので、数値的に”近似値”を計算することが必要になります。

関数 f(x) の形や数値が与えられた場合、その導関数 f '(x) を計算することは、微分の定義に戻って考えると

f '(x) = lim (h -> 0) f₁(x,h) ... f₁(x,h) = ( f (x+h) - f(x) ) / h

なので、f₁(x, h) を f '(x) の近似として採用するのが自然です。刻み幅 h をできるだけ小さくとれば、次第にその値は f '(x) に近づくことが期待できます。例として f(x) = sin(x) に対して、 h = 1/2ⁿ とした場合の計算値と f '(x) = cos(x) の誤差を評価してみましょう。次のプログラムリストに x を入力したときに h に対する誤差を出力するプログラムを示します。

program main  
  implicit none 

  real x,h                  ! 変数宣言
  real df,df0
  integer n
  character(len=10) fname   ! 文字の宣言 : len 以下は文字数

  write(*,'(a,$)') 'x ? '         ! 画面に x? と表示
  read(*,*) x                     ! 画面に打ち込んだ x を読み込む
  write(*,'(a,$)') 'file name ? ' ! 画面に file name? と表示
  read(*,*) fname                 ! 画面に打ち込んだ file name を読み込む  

  open(10,file=fname) ! ↑で名前を付けた file を開く

  do n=0,20
    h=1.0/(2.0**real(n)) ! **n : n乗のこと。
    df=(sin(x+h)-sin(x))/h ! 数値的な微分（一次精度）
    df0=cos(x)             ! 解析的な微分 (手計算)
    write(10,'(2e15.8)') h,abs(df-df0) ! abs( ) : 絶対値
  end do

  close(10) ! file を閉じる


end program main

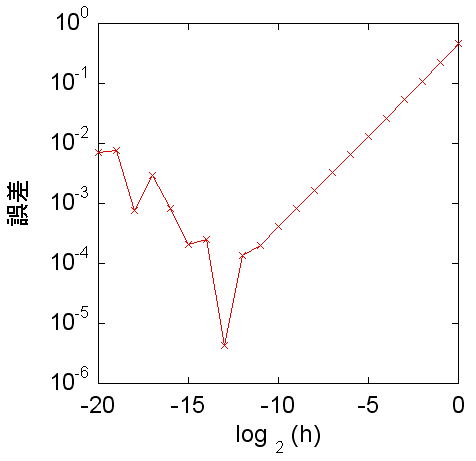
結果をグラフにしてみましょう。予想では h が小さくなるのに対して誤差も小さくなるはずでしたが、結果は h　がある程度小さくなるとそこから先はかえって誤差が増加します。これはどうしてでしょう？

結論からいうとこれは計算機が扱う数は桁数が有限であることに起因します。数値計算の誤差には2つの種類があります。(1) 打ち切り誤差　と (2) 丸め誤差 です。

(1) 打ち切り誤差

打ち切り誤差とは「本来無限桁数の計算をしなければならないものを有限桁数で打ち切ることによって生じる誤差」のことです。 f(x) を x の周りでTaylor展開すると導関数 f '(x) の打ち切り誤差は

f₁(x) - f '(x) = h f "(x) / 2 + O(h²)

となります。この誤差は h　が小さくなるにつれて減少するはずです。

(2) 丸め誤差

丸め誤差とは「実際の実数とその最も近い浮動小数点表現との差」のことです。

仮数部が24 bitの浮動小数点表現をした場合の数 a は、計算の際に a * 2^-24 程度の誤差を持つことになります。このような誤差を持つと、２つの絶対値の非常に近い数の加算または減算を行った結果が０に極めて近い値をとるような場合に、絶対値が減少しただけ相対誤差が増加して有効桁数が著しく減少することになります。今問題にしている f(x+h) - f(x) の計算の場合はまさにそのような状況であり、f(x) や f(x+h) の誤差がδ程度あったとすると f₁(x) を計算する際の丸め誤差は

〜 2 δ/h

程度になります。δは一定の値で h　の値をどんどん小さくしているのですから、この誤差は h を小さくするにつれて増加することになります。したがって、(1) と (2) の誤差から 「h は大きすぎても小さすぎてもいけない！」という結論が導かれます。

導関数の誤差の全体は

（誤差）　= h | f "(x) | /2 + 2 δ/ h

となります。したがって、誤差を最小にする h　は

h = 2 ( δ/ | f "(x) | )^1/2

と評価できます。例えば上の例の場合、| f "(x) | 〜1 で、δ〜2^-24なので、 h 〜 2^-11となります。グラフに示した結果の傾向をよく説明できていることがわかります。

精度の改善 〜その1：　丸め誤差対策

精度をあげる一つの方法は、より小さな h での計算を許容できるように丸め誤差が小さな実数表現を利用することです。これまでの計算で、実数は "real" という型で宣言していました。この実数型は仮数部24 bitの4 byteの浮動小数点形式です。これより高い精度を必要とする場合は、倍精度実数型という型が用意されています。これは仮数部53 bit の8 byteの浮動小数点形式になります。宣言の方法は "real(8)" または "real(kind=8)"です。（注：通常の実数を倍精度に対応して単精度と呼ぶことがあります。"real(4)"または"real(kind=4)"と宣言することもできます。）　倍精度では 2^-53 までの精度で数値を表現できるので、h 〜 2^-26 に最適な h　をとることになります。

精度の改善 〜その2〜：　打ち切り誤差対策

これまで用いてきた f '(x) の近似値 f₁(x) は h f "(x) 程度の誤差を持つので、 h の1次精度を持つといいます。x の近傍の他の f の値を用いることによって、打ち切り誤差のより小さな導関数の計算方法を構成することができます。

f (x+h) = f (x) + h f '(x) + h² f" (x) / 2! + O(h³) ... �@

f (x-h) = f (x) - h f '(x) + h² f" (x) / 2! + O(h³) ... �A

�@-�A　を計算すると

f₂(x,h) = ( f (x+h) - f (x-h) ) / 2h = O(h²)

となり、 h の2次精度の差分近似式が構成できます。

打ち切り誤差は　f₂(x) - f '(x) = h² f ⁽³⁾ (x) / 6 + O(h⁴)

丸め誤差は　2 δ/ 2 h = δ/ h

したがって、h の最適値は　（誤差） = h² f ⁽³⁾ (x) / 6 + δ/h を最小にするものなので

h = ( 3δ/ | f ⁽³⁾ (x) | )^1/3

2次精度の微分式は、1次精度の微分に比べて h の最適値が大きくなっていることに注意してください。しかし、結果の有効桁の精度は1次精度の場合よりよくなっていることがわかります。

program main
  implicit none

  real x,h
  real df,df0
  integer n
  character(len=10) fname

  write(*,'(a,$)') 'x ? '
  read(*,*) x
  write(*,'(a,$)') 'file name ? '
  read(*,*) fname

  open(10,file=fname)

  do n=0,20
    h=1.0/(2.0**real(n))
    df=(sin(x+h)-sin(x-h))/(h*2.0)　　　←　★ ! 二次精度
    df0=cos(x)
    write(10,'(2e15.8)') h,abs(df-df0)
  end do

  close(10)

end program main

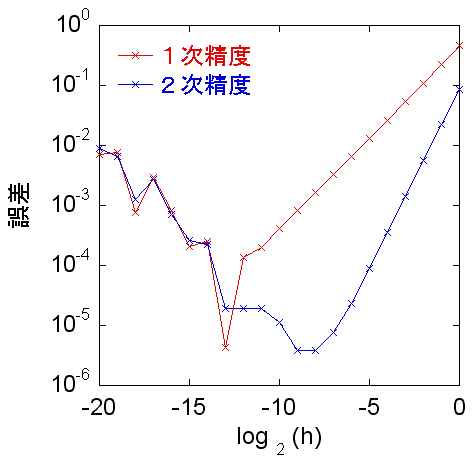
同様な方法で　f (x+2h), f (x-2h), f (x+3h), f (x-3h) などを導入すると、より高次精度の近似式を構成できます。これは課題とします。

○ 課題

(1) f(x+2h), f(x+h), f(x-h), f(x-2h) を使って 4次精度の微分公式を、 f(x+3h), f(x+2h), f(x+h), f(x-h), f(x-2h), f(x-3h) を使って 6次精度の微分公式を導出してください。

(2) 4次精度、6次精度の微分公式を使って数値微分を実行し、最適な刻み幅 h の大きさを評価してください。

(3) 倍精度　の実数を使った数値計算を行い、微分精度がどれ程向上するかを評価してください。