・数値積分法

微分については解析的に求めることができても、一般的に微分に比べて積分は限られた場合にしか求まらないことが多い。 それ故、数値積分が必要とされる場面は多い。まずは簡単に１次元の定積分について考えてみよう。

定積分

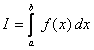
の積分区間 [a,b] をN分割して、関数 f(x) で囲む領域を台形で近似して面積を求めることが、 最も簡単な I の近似となる。h=(b-a)/N と表すと

f(x) が解析関数であれば、数値積分の誤差は Euler-Maclaurin の公式から

aはhに依存しない定数と表される。 したがって、刻み幅 h を半分にすると、おおよそ誤差は 1/4 になることがわかる。

高次精度化 - Richardson 補外

誤差評価の式から

を定義すると

なので、同様の操作を繰り返せば高精度公式

を導くことができる。(Richardson補外）特に、k=1 の時に

Simpson則 の式が導かれる。

以下に台形公式から exp(x) を区間 [0,1] で数値積分を求める為のサンプルプログラムを示す。

1 program integ1
2   implicit none
3 
4   real a,b,h,x,s,s0
5   integer n,i
6 
7   write(*,'(a,$)') 'input N ' ! * : 画面上に表示 / 区間[0,1]を幾つに割るか
8   read(*,*) n                 ! * : 画面上から読み込み  
9 
10  a=0.0  
11  b=1.0 
12  h=(b-a)/real(n) ! n は 元々整数なので 実数に直す
13                  ! ※計算に使う変数の型は全て合わす
14  s=(exp(a)+exp(b))/2.0   ! s1 = 1/2 (f(a)+f(b))   
15  do i=1,n-1
16   x=a+real(i)*h  ! i は 元々整数なので 実数に直す
17   s=s+exp(x)     ! s2 = s1 + f(a+h) + f(a+2h) + ...   
18  end do
19  s=s*h           ! s3 = s2*h / これが数値的な積分 
20
21  s0=exp(1.0)-1.0 ! 解析的な積分（手計算）
22
23  write(*,'(a,e20.10,a,e20.10)') 'I=',s,'   error=',s-s0 ! * : 画面上に表示
24
25 end program integ1

○課題

(1) 数値微分の時と同様に N を大きくしていった時に、数値積分の精度がどうなるか考察してください。

(2) Richardson補外で数値積分の精度が改善されることを確認してください。